ボッテマの定理

ユークリッド幾何学において、ボッテマの定理（ぼってまのていり、英語: Bottema's theorem）とはオランダの数学者オーネ・ボッテマ（フローニンゲン, 1901–1992）にちなんで名づけられた定理である。

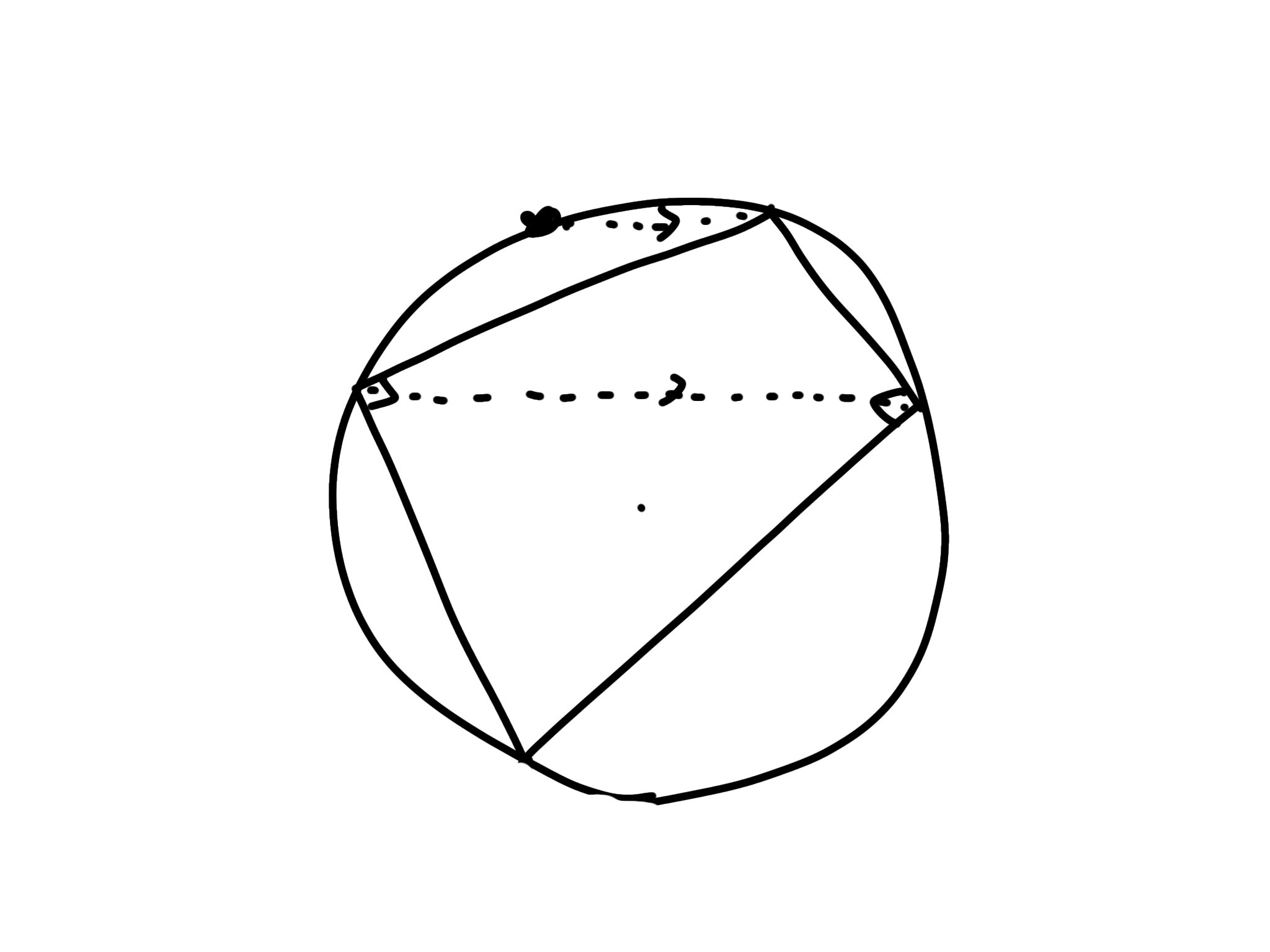
三角形 ${\textstyle ABC}$ についてそれぞれ ${\textstyle AC}$ , ${\textstyle BC}$ を一辺とする正方形を外側に描く。このときそれぞれの正方形の、 ${\textstyle C}$ と反対の点を結んだ線分の中点 ${\textstyle M}$ は ${\textstyle C}$ の位置に依らない。

また ${\textstyle M}$ は、辺 ${\textstyle AB}$ の中点を ${\textstyle S}$ とし ${\textstyle AS=BS=MS}$ を満たす三角形の内側の点、つまり ${\textstyle \angle MAB=\angle MBA=-{\frac {\pi }{4}}}$ を満たす点となる。

ボッテマの定理は内側に正方形を描いたときも同様に成り立つことが知られており、このとき ${\textstyle M}$ は ${\textstyle AS=BS=MS}$ を満たす三角形の外側の点、つまり ${\textstyle \angle MAB=\angle MBA={\frac {\pi }{4}}}$ を満たす点となる。

更に、ボッテマの定理は任意の正多角形に一般化できる。

三角形 ${\textstyle ABC}$ に、それぞれ辺 ${\textstyle AC}$ , ${\textstyle BC}$ を一辺とする正多角形を外側あるいは内側に描く。また正多角形の外接円上の頂点 ${\textstyle C}$ の対蹠点をそれぞれ $D_{1}$ , $D_{2}$ とする。この時、 $D_{1}D_{2}$ の中点は ${\textstyle C}$ の位置に依らない。